仁信配资-正规配资官网-股票可以杠杆-正规配资

114配资网可你有没有想过一个问题：有没有一种刚性几何形状

如果你随手捡起一个四面体形状的小玩具，扔到桌子上，它会落在哪一面？多数人可能会觉得这是个无聊的问题：不就是随机的吗？但数学家的脑回路和我们不太一样，他们会继续追问：

有没有可能造出一种四面体，它不论你怎么扔，总是落在同一面上？

这不是“加重底部”的那种不倒翁玩具吗？你可能会这样想。没错，圆形的不倒翁通过重心调整可以做到“永远翻回原位”。但如果我们不使用圆滑的曲面，只用最原始的平面+棱角——也就是数学中所谓的多面体，还能做到这点吗？

这就变成了一个真正有挑战的问题：有没有可能造出一个由硬质材料构成的四面体，它只能在某一个面上稳定下来？

60年前，传奇数学家约翰·康威（John Conway）曾提出过这个问题，并表示直觉上觉得答案是“有可能”。但直到他去世，也没人能真正造出这样的物体。

一个四面体，四个面，四种可能落点。你得想办法让它的几何结构和重量分布如此精妙，以至于其他三个面一旦接触地面，都会自动“翻”到那个唯一的面上。这个问题乍一看像是玩具设计，却牵扯到几何结构、物理稳定性、质心位置、材料密度等多种因素的高度耦合。

它简单得像个脑筋急转弯，又复杂得像一个时代的未解之谜。

而如今，这个问题终于被解开了。不是靠复杂的方程，而是靠直觉、算法，还有几滴精密胶水。

从柏拉图到康威，形状中的大问题

公元前四世纪，哲学家柏拉图提出了一个如今看来带着神秘色彩的构想：他认为宇宙是由五种几何体构成的，每一种都象征着一种基本元素——火、土、水、气与宇宙以太。支撑他这个宇宙观的，是五种完美的三维形状，后世称为柏拉图立体（Platonic solids）：四面体、六面体（立方体）、八面体、十二面体和二十面体。

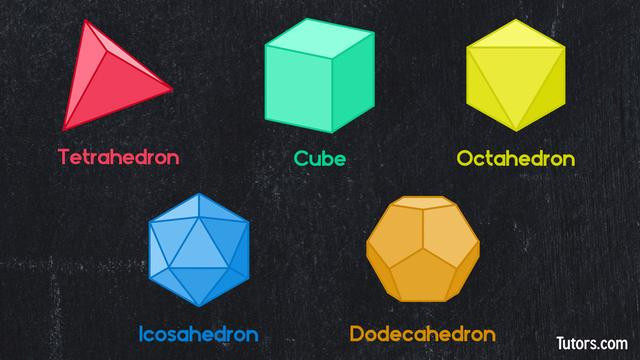
其中，四面体是最简单的一种：四个完全相同的等边三角形面，每个顶点连接三个面。它是“纯粹几何”的开端，也是所有三维多面体中的最小单位。这种极简之美使它自古便成为几何学探索的起点，数学家对它的兴趣，跨越了两千多年，至今未减。

然而，四面体的简单外形背后，隐藏着意想不到的复杂性。比如：如果你拿一堆完全相同的正四面体，能不能像堆积木那样，把它们紧密地填满一个空间？这个问题直到21世纪还未彻底解决。

又比如：能不能把一个任意形状的四面体切成若干块，再重新拼成一个正方体？这个看似动手能力的问题，实则触及到了体积保持与空间重构的深层规则。

在这样的问题谱系中，还有一个更加微妙却长期被忽视的问题：一个四面体可以“稳定”地站在几个面上？

这个问题真正进入数学家的视野，是在1966年。当时，两位极富创意的数学家——约翰·康威（John Conway）与理查德·盖伊（Richard Guy）——开始研究多面体的“平衡状态”问题。他们并不满足于研究四面体的体积、角度、堆砌方式，而是开始问一些“姿势”层面的问题：如果把一个四面体随意放在桌子上，它会如何落地？会在哪一面停下来？有没有可能设计一种形状，让它只能停在一个特定的面？

他们最初限定了条件：材料必须是均匀分布的，即质量密度在整个形状中处处一致。他们证明，在这种限制下，是不可能实现“单稳态”的四面体的——它一定会有至少两个或以上的稳定面。

这个负面结果本应使得问题就此封尘，但数学的魅力正在于此：一旦你放宽某个限制，整个世界就重新开放了。

康威留下了一个更大胆的问题：“如果我们允许材料的密度不均匀，是不是就有可能造出一个只能稳定在某一个面上的四面体？”

这个问题没有被正式发表，也没有留下任何手稿证明。它像是康威在无数脑洞之间随口一提，却在少数几位后来者心中埋下了种子。它既不宏大，也不炫技，甚至不需要高等数学，却精准地击中了几何世界的一块盲区。

有时候，真正重要的问题，并不是那些看上去伟大的，而是那些令人困惑的小问题，在悄悄挑战你对“简单”二字的理解。

Gömböc：数学界的“不倒翁”

在日常生活中，我们都见过那种可爱的“不倒翁”：不论从哪个方向推它，它总会晃晃悠悠地站回一个固定的位置。这种玩具的原理说来简单——底部加了重物，使得重心极低，因此总能自动翻回原位。可你有没有想过一个问题：有没有一种刚性几何形状，不依靠任何外部配重，光靠自身结构，就能做到类似“不倒翁”的行为？

这个看似童趣的问题，在数学界却引发了一场真正意义上的“结构革命”。

2006年，匈牙利布达佩斯科技大学的数学家Gábor Domokos，联手工程学者Péter Várkonyi，成功设计并构造出一种神奇的三维形状——Gömböc（音：贡博茨）。这个名字源于一种匈牙利的圆滚滚食物，但它的数学性质远比名字更“硬核”：它是第一个已知的均质、凸的三维物体，只能在一个点上稳定平衡，在另一个点上不稳定平衡，其余任何位置都会自动翻转。

用更专业的语言来说，Gömböc 是一个mono-monostatic 体：一稳定、一不稳定、无其他中间态。

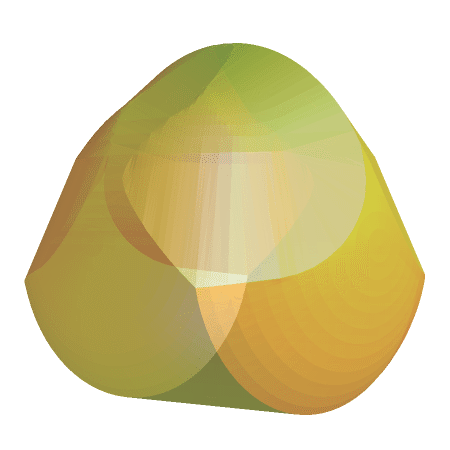
这听起来不可思议，但确实存在。在此之前，数学家普遍认为这样的物体几乎不可能出现，因为它必须同时满足以下几个苛刻条件：

整体质量均匀分布，不能靠内部加重作弊；

整体是凸体，没有凹陷或内部空腔；

结构要在拓扑上保持连续和平滑；

只能有一个稳定和平衡点，且不能有多余的“假平衡”状态。

Gömböc 的发现不仅是一种数学上的突破，更是一种物理与几何边界的重新界定。它打破了人们对物体“稳定性”的直觉设限：原来不靠配重、不靠刻意凹槽，只靠形状本身的“几何布设”，就能引导物体的动态趋向于某个确定姿态。

这个形状的出现，也迅速引发了其他领域的关注。生物学家注意到，某些乌龟的背壳形状非常接近 Gömböc，这或许是它们能够在翻覆后自己翻回来的自然选择结果；在工程领域，Gömböc 激发了关于“自动复位结构”的新构想，譬如地震中能自己回正的建筑构件、或自动扶正的深海探测器。

更重要的是，Gömböc 提出了一个新的数学问题：既然“圆滑”的形状可以做到单稳态，那么有没有可能，多面体——那些棱角分明、面数有限的形状，也能做到这一点？

这是 Domokos 心中的一个未解梦魇。他清楚，Gömböc 虽然美妙，但它依赖的是连续曲面的调和，而多面体的几何世界，是离散的、断裂的、无法轻易“平滑处理”。可也正因为这样，问题才更有趣：单稳态，是Gömböc的专利，还是形状世界的普遍可能？

这时，他开始回忆起康威提出的那个被遗忘了几十年的小问题。而这，便成为另一段探索的起点。

AI + 手工：学生找到的“魔法坐标”

2010年代末，布达佩斯科技大学的教室里，坐着一个沉默寡言的年轻人。他不是数学系的，也没有发表过什么论文。Gergő Almádi，一名建筑专业的本科生，只是因为对结构感兴趣，选修了一门力学课，授课老师叫做Gábor Domokos。

这门课看起来平平无奇，却悄然点燃了一个几何学爆点。

课程结束时，Domokos留了一个特别的项目作业：设计一个算法，用来探索“四面体落在哪面”的问题。他没有多讲，只是鼓励学生用程序试试看。对大多数人来说，这只是个附加练习，但对 Almádi 来说，却像是一个暗门：既然现实中的物体会“翻身”，能不能用计算机来反推哪些形状具有这种特性？

他开始编程。不同于传统的数学证明方式，Almádi采取了穷举 + 几何规则 + 模拟重心的组合手法。他的程序在虚拟空间中快速生成各种略微“扭曲”的四面体形状，逐一测试：每次改变边长、角度、质量分布，然后模拟形状从各个面落地后的动态行为。

这个过程就像在黑夜里摸宝，绝大多数模型都“不稳定”得一塌糊涂：要么能站稳好几个面，要么干脆四仰八叉。但 Almádi 并不气馁。程序日复一日地跑着，坐标数据如雪崩般滚来。

直到某一天，屏幕上出现了一个奇怪的例子：四个顶点的三维坐标构成了一个异形四面体，当它在特定重心分布下，总会最终“翻滚”到同一面，无一例外。

换句话说，这个形状在理论上达到了“单稳态”。

他激动地把结果发给了 Domokos。后者一看数据，几乎立刻意识到，这不是偶然，而是几十年前康威猜想的一个潜在实证。这个年轻人，居然在没有预设公式、没有传统工具的情况下，用暴力算法找到了一种前所未有的几何构型。

坐标已经找到——每个点在三维空间的位置都明确无误。下一步，就是要回答一个更有挑战性的问题：

这个形状，只是数学模型里的理想体，还是可以被真实制造出来？

不过，哪怕抛开实体构造的问题，仅从算法角度，Almádi 的突破已经非同寻常。因为他不仅找到了一个解，还为后续研究指出了一个新的探索方向：

——有没有更多的“单稳态四面体”？它们是否拥有某些共同几何特征？能不能反过来，从这些特征出发，缩小搜索范围？

这不再是一个人在电脑前孤独敲代码的问题，而是牵动整个形状理论的重构提案。从一组神奇的坐标开始，一场几何新探索，悄然展开。

造出来了！但为什么这么难

纸上谈兵是轻松的。坐标有了，重心位置精确，仿真模拟显示——它会翻滚到某一面，然后稳定不动。听起来，只要照着三维模型打印出来，不就大功告成了？

现实却狠狠泼了一桶冷水。

要让一个几何形状只落在一个面上稳定，容不得任何一点偏差*哪怕是一根棱线轻微翘起，哪怕一面略微变形，哪怕一滴胶水的位置偏了，它就会在别的面上“卡住”，彻底失去单稳态特性。

这是一个精度要求高到近乎偏执的工程问题。

数学家 Gábor Domokos 和学生们最初按坐标打印出一个模型时，它根本不能如愿翻转。他们以为哪里算法出了错，又检查了一遍遍公式、模拟、数据。直到某一天，一位工程师无意中发现：模型某一顶点处，有一小坨胶水多涂了一点点。那点胶水虽然只有几克重，却悄悄移动了整个结构的质心，最终导致它落在错误的面上“僵住”。

那一刻，他们终于意识到：这不是模型错了，而是“太真实”了。

于是，新的工程挑战展开：

材料选择必须极端轻与极端重巧妙搭配。结构主体选用中空碳纤维壳，尽可能减少自身重量；

配重部分选用碳化钨（tungsten carbide），一种比铅还重的金属，来构建内部的“引力核心”；

每一面粘合时使用的胶水量都要精确计量，连涂抹的位置也必须记录；

整体模型的误差控制在0.1克以内、0.1毫米以内。

他们联系了一家位于匈牙利的精密制造公司，展开了漫长的试制过程。每一次失败都伴随着某个看不见的小问题：一个连接处的微弯，一块板材受力不均，一道表面粗糙度超限。这些“非数学”的因素，统统成了拦路虎。

期间甚至发生过“全套已制完，最后不动”的惨剧。一整块材料报废，只因模型在运输中略受压迫，导致某一内角稍有变化。

最终，经过数月反复打磨与调整，他们做出了一件看似平平无奇的小物体——四面体，50厘米长，120克重，外壳轻盈如羽，内部沉稳如铁。